what property of a substance corresponds to the average potential energy of its particles
Properties of pure substances
Backdrop
Substances take backdrop that are used to identify and depict them. You should be familiar with four properties from everyday life: temperature, pressure, book and mass. Nosotros measure the amount of milk by volume and meat past mass. Nosotros quantify the "hotness" or "coldness" of air by measuring its temperature. Pressure gives an indication of the force necessary to incorporate a fluid.
We distinguish between intensive and extensive properties. Temperature is an intensive property as its value does not depend on the corporeality of matter of the substance. A cup of water tin can exist at twenty\(^\circ\)C as well as a drop of water. Volume and mass are extensive properties. The mass and volume of a substance is directly proportional to the amount of matter making up the substance. A loving cup of h2o cannot take the aforementioned mass equally a drib of water.
Another characteristic of properties is that the value of a holding at the present is not dependent on the history of the substance. The temperature of a loving cup of water at the nowadays moment is not dependent on its temperature a few minutes ago. The water could accept been colder or hotter at a previous phase. Therefore, properties are called indicate functions. Distance on the other hand, is a path part every bit the altitude traveled to get from point A to point B, is dependent on the path followed. Work performed and oestrus transferred are likewise path functions equally volition become clear later.
Temperature
Temperature is measured in degrees Celsius [\(^\circ\)C] or Kelvin [Thousand]. To convert a temperature in \(^\circ\)C to Yard, add 273.15. This means fifty\(^\circ\)C is the aforementioned equally 323.15K. It also means that a temperature difference expressed in degrees Celsius is numerically the aforementioned every bit the divergence expressed in Kelvin. The everyman possible temperature is 0K. Temperature is an intensive variable.1
Pressure level
Pressure (\(P\)) is the pressure level: \[P = \frac{F}{A}\]
With F in [\(kN\)] and A in [\(m^two\)], P will be in [\(\frac{kN}{grand^2}\)]=[\(kPa\)]. Pressure is an intensive variable.
Other common force per unit area units are:
-
temper (\(1 \mbox{atm} = 101.325 kPa\)) and
-
bar (\(1 \mbox{bar} = 100 kPa\))
Absolute or total pressure
The full pressure is the full forcefulness exerted on a surface divided past the area of the surface. In a gas, the strength exerted on a surface is due to the collision of the gas molecules against the surface. In that location is a limit at how low total pressure level tin be. If no strength is exerted on a surface the total pressure is zero. The pressure of a complete vacuum is zero because there are no molecules colliding with the surface of the container. Absolute pressure (\(P_{abs}\)) is the pressure measured in a higher place this cypher point. The value of full pressure can never be negative.
Atmospheric pressure
Atmospheric force per unit area (\(P_{{atm}}\)) is the total pressure level caused past the weight of the atmospheric air. This pressure level varies co-ordinate to location and conditions patterns. The average value at sea-level is \(101.325kPa\). The average atmospheric force per unit area for Potchefstroom is \(87.0kPa\) and \(99\%\) of the fourth dimension the pressure volition be between \(86kPa\) and \(88kPa\). The average atmospheric pressures for a few major cities in S Africa are given in Table 2.1.2 It is clear that the meridian above sea level plays a very important role in determining the average value.3 Atmospheric pressure is also called ambient pressure.
| Metropolis | Tiptop in a higher place ocean level [\(m\)] | Hateful atmospheric pressure [\(kPa\)] |
|---|---|---|
| Kimberley | 1230 | 88.5 |
| Polokwane | 1262 | 88.iii |
| Pretoria | 1350 | 87.5 |
| Potchefstroom | 1351 | 87.0 |
| Bloemfontein | 1395 | 86.7 |
| Johannesburg | 1700 | 83.5 |
Estimate pressure
Gauge pressure level (\(P_g\)) is the divergence between the total pressure inside the vessel and an the full pressure outside. \[P_{gauge}=P_{within}-P_{{outside}}\] Normally the total pressure exterior is equal to atmospheric pressure simply for a vessel submerged in h2o such every bit a submarine, or the air cylinder of a Scuba diver, the total pressure level exterior may differ from the atmospheric pressure. If the pressure inside is lower than the force per unit area outside, the approximate pressure will be negative and when it is higher, it will be positive. Except when specifically stated that information technology is a full or absolute force per unit area approximate, the pressure displayed by a pressure level gauge is the gauge pressure. We apply a pressure gauge at the petrol station to measure the gauge pressure of the air in the tires of our cars.
Instance
Presume you have inflated the tyres of your car to a guess pressure of \(200kPa\) on the Highveld where the atmospheric pressure level on that 24-hour interval is \(85kPa\). The absolute (or total pressure) inside the tyres is now \(285kPa\). You at present drive to the ocean where the atmospheric pressure on that day is \(101kPa\). What is the gauge force per unit area of the tyres at present?
Solution
If the tyre does not leak, the mass of air within does non change. Let us assume the volume stayed the same as well as the temperature. Therefore the absolute pressure level inside the tyres as well remained the aforementioned (this can exist shown to be true by using the Ideal Gas Law which is done later on), only the guess pressure level would have dropped to 184kPa. In lodge to suspend the weight of your car at this lower pressure, a bigger area is required and your tyres will announced a petty flatter than at the highveld. You will have to inflate the tyres.
Hydrostatic Pressure
The pressure exerted by a liquid column with a uniform density, is given past the equation:
\[P=\frac{\rho k h}{1000}\]
With \(\rho\) in [\(\frac{kg}{thou^3}\)], \(yard=9.81\frac{m}{s^ii}\) and h in [\(g\)], P will be in [\(kPa\)].
Example Presume you go downwards a mine shaft \(1000m\) deep. Calculate the pressure exerted by a column of air \(1000m\) high. Assume the air has a constant density of \(one\frac{kg}{k^3}\).
Solution \[P=\frac{i\times9.81\times 1000}{thou}=9.81kPa\] This is in the same range as the alter in pressure y'all will experience traveling from the Highveld to the coast. The density of the air volition change due to the significant alter in pressure - so the assumption of compatible air density can be questioned. How will you account for the change in air density?
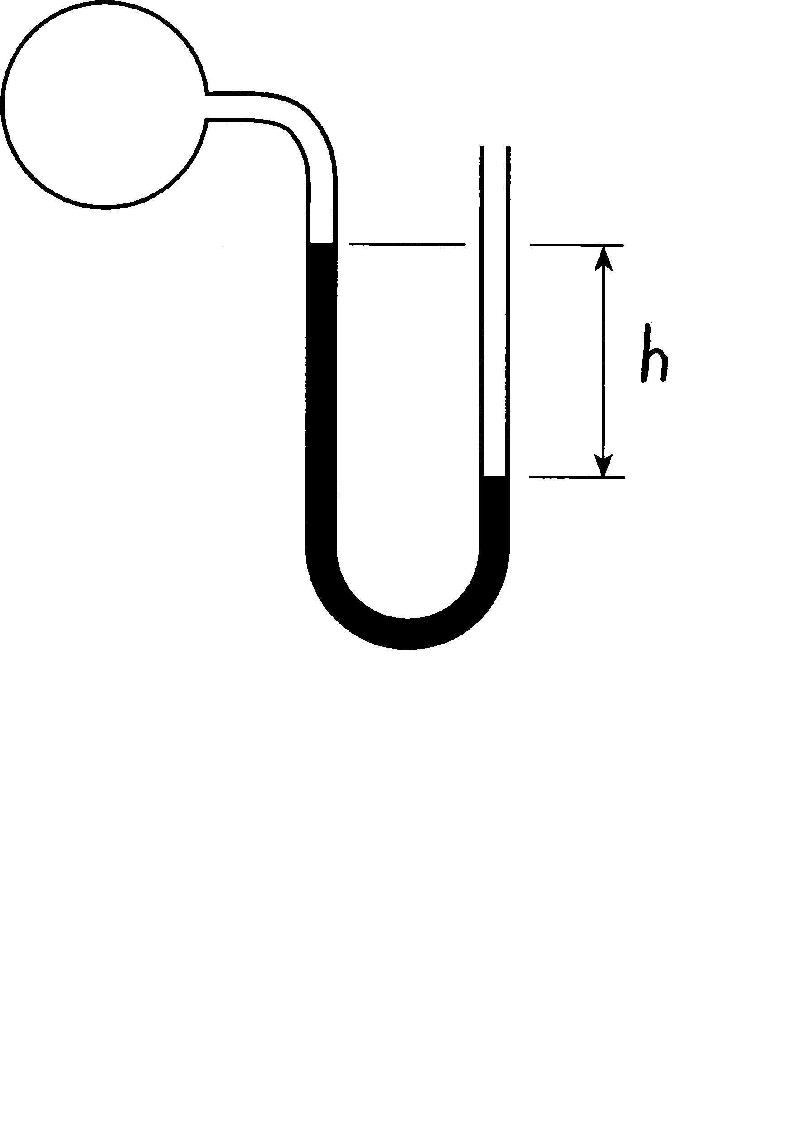
Effigy 2.1: Manometer
Example
A sectional view of a U-shaped manometer filled with mercury connected to a pipe filled with air is shown in Figure 2.one. The departure in height of the mercury in the legs of the manometer (h) is \(0.2m\). The density of the mercury can be taken as \(13600\frac{kg}{m^iii}\) and the atmospheric pressure as \(87kPa\). Calculate the absolute and gauge pressure inside the pipe.
Solution
The pressure exerted past a cavalcade of mercury with height \(h\) is: \[P_{mercury}=\frac{0.2 \times 9.81 \times 13600}{1000}= 26.68kPa\] The force per unit area on the surface of the mercury exposed to the atmosphere is equal to \(87kPa\). In the other leg of the manometer, at the same superlative, the pressure will besides be \(87kPa\). Moving upwards from that elevation to the surface of the mercury, will crusade a drop in total pressure. Therefore:
\[P_{abs,inside}=87-26.68=58.32kPa\]
The density of the air is very low, therefore information technology can be causeless that the pressure inside the piping is uniform. The gauge pressure is \(-26.68kPa\). From the relative height of the mercury columns in the legs of the manometer it is also clear that the force per unit area inside the pipage is lower than the pressure inside, therefore information technology makes sense that the guess pressure has a negative value.
Volume and Mass
It is often convenient to combine the two all-encompassing properties, book and mass, to form an intensive holding: specific volume (\(v\)). Specific book is the full volume divided by the total mass \(5=\frac{Five}{m}\) [\(\frac{m^iii}{kg}\)]. Specific book is an intensive property. Density (\(\rho\)) is the inverse of specific volume.
Case
A loving cup holds \(250m\ell\) of boiling hot water at \(95^\circ C\). The mass of the water is \(240.4g\). Calculate the specific volume in [\(yard^3/kg\)] and the density in [\(kg/m^3\)].
Solution Specific book is the total volume divided by the total mass: \(v=V/m\). Commencement determine the values of \(V\) and \(grand\).
\[\brainstorm{aligned} 5 &= 250m\ell \times \frac{1\ell}{1000m\ell} \times \frac{1m^3}{chiliad\ell} \\ &= 250 \times x^{-six} g^3 \\ m &=240.4g \times \frac{1kg}{1000g}\\ &= 240.4 \times ten^{-3} kg\\ \therefore v &=\frac{250\times x^{-6}}{240.4 \times 10^{-3}}\\ &= 0.00104 \frac{m^3}{kg} \\ \mbox{and} \, \rho &=\frac{ane}{v} = 961.5 \frac{kg}{m^3} \end{aligned}\]
Sometimes the density of a substance is given relative to a reference substance. So it is called relative density or the somewhat misleading term, specific gravity (SG). In the case of liquids (and often solids) the reference substance is usually h2o at a pressure level of \(101.3kPa\) and \(four^\circ C\) with a density of \(k \frac{kg}{m^3}\). The SG of mercury is usually taken equally xiii.6. This means its density is \(13600\frac{kg}{chiliad^3}\)
Let us run into how \(P,T\) and \(v\) are interdependent.
Single phase systems
The term phase refers to a quantity of matter that is homogeneous throughout in both chemical limerick and concrete structure. Homogeneity in physical structure ways that the matter is all solid, or all liquid, or all gas. An oil-water mixture consists of two liquid phases - a h2o phase and an oil phase. They are both liquids merely their chemic compositions differ. The 3 phases of water are shown in Figure 2.2 below. The three phases are separated by phase boundaries with cypher thickness - although to be able to run into it on the graph, a line with finite thickness must be used, otherwise the line would accept be invisible.4 It means that when you specify the value of temperature and the value of pressure, that the indicate can never fall on the line. For instance for \(P=87.00kPa\) and \(T=95.78^\circ C\) water will be a liquid and at the same pressure but a slightly college temperature of \(T=95.79^\circ C\) it will be a gas. Y'all can use as many digits as yous desire to, the water will be either a liquid or a gas. (Peculiarly doing calculations using software, it is easy to forget this.) It will become clear afterwards that the lines in Figure two.two represents two-phase mixtures, either liquid/gas, liquid/solid or solid/gas.
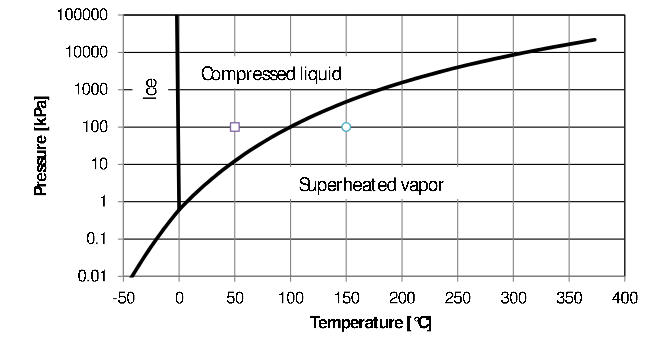
Figure 2.two: The three phases of water
For single-phase substances, we can modify the values of two intensive properties independently - in other words, a change in temperature for instance, volition non necessarily lead to a change in pressure level (as long as we stay clear of the phase boundaries!) For instance, consider liquid water at \(100kPa\) and \(50^\circ C\) (indicated by the \(\Box\)). When we heat a cup of cold water in the microwave oven, nosotros increase the temperature while the pressure level exerted by the atmosphere on the h2o remains constant. When we put the cup in a refrigerator, the temperature will now drib but the pressure will not alter. Nosotros tin too vary the temperature and pressure of steam (shown past the \(\circ\)) independently of each other.
Because we can alter the value of two intensive properties independently we say a single-phase substance has two degrees of freedom.v Information technology means that we just have to specify the values of 2 independent intensive properties in guild to ready the state of the system and the values of the other intensive properties. The state of the substance is simply the status of the substance equally described by its properties. If we heat upward water, we say its state has changed because its temperature has changed. There are different ways in which to make up one's mind the value of the other backdrop.
Ideal gases
An ideal gas is a hypothetical gas whose molecules/atoms exercise not attract or repulse each other and collide elastically with each other and the walls of the container. They are point particles occupying negligible space. At loftier temperatures and low pressures,half dozen the density of gases are low (the particles will occupy negligible infinite) and the kinetic energy of the particles much higher than any possible inter-particle interactions. Under these conditions gases approach ideal gas behavior. For an Ideal Gas, the relationship betwixt the force per unit area, temperature and total book are given by the Ideal Gas Police: \[PV=north\overline{R}T\] where \(\overline{R}\) is the universal gas constant with a value of \(8.3145 \frac{kPa\cdot m^3}{kmol \cdot K}\). Information technology is of import to note that the molecular mass of the gas under consideration does not play a office in this equation. A kilomole of Helium and and a kilomole of Air at the aforementioned pressure and temperature will occupy the same book - at \(25^\circ C\) and \(100kPa\) that volume will be \(24.8m^iii\) although the Helium volition counterbalance 4kg and the Air 28.97kg. This means a balloon filled* with one kmole of Helium will exist able to elevator a mass of about \(25kg\). The diameter of such a spherical balloon volition be \(3.4m\).7
In Engineering we prefer working with mass. The Ideal Gas Law is rewritten as \(PV=mRT\) with \(R=\frac{\overline{R}}{MM}\). MM is the molecular mass, and \(R\) is the ideal gas constant for the substance under consideration. Its units are \([kPa\cdot m^iii\cdot kg^{-1}\cdot K^{-1}]\) and it has a specific value for every substance. The platonic gas abiding for iii substances are shown in the Table 2.2 beneath.
| Substance | R |
|---|---|
| Air | 0.2870 |
| Steam | 0.4615 |
| Helium | 2.0771 |
Tables with the values of the ideal gas constant for different substances tin can exist plant in literature (Table A.5).8 (Sonntag and Borgnakke 2012). It is ofttimes convenient to work with specific volume and the Ideal Gas Police so becomes: \[Pv=RT\]
An ideal gas is a single phase substance and according to the Gibbs phase dominion, has two degrees of freedom. This is also clear from the Platonic Gas Constabulary that one time we know what the values of the temperature and pressure are, we tin calculate the specific volume. If fact if we know the values of any two variables (\(P,T\); \(P,five\); \(T,v\)) we say the state is fixed and we can summate the value of all other intensive properties.
Instance
Consider air at \(25^\circ C\) and \(101kPa\). Calculate its specific volume and the mass of \(1m^three\) of air.
Solution
\[\brainstorm{aligned} v &= \frac{RT}{P} \\ &= \frac{0.287\times298.fifteen}{101} \\ &= 0.8475 \frac{m^3}{kg}\\ \\ m &=\frac{V}{v}\\ &=\frac{one}{0.8475}\\ &=one.180 kg\\ \cease{aligned}\]
Make certain of the units when using the Ideal Gas Law. Temperature is in Kelvin, pressure is the absolute pressure level in \(kPa\) and specific volume is in \(one thousand^3/kg\). In the case of gases similar air in everyday use and Helium, the Ideal Gas Police force is quite accurate.
In this notes, Helium and Air are always treated every bit platonic gases.
Real Gases
Super-heated steam is usually considered to be a real gas9 and the specific volumes at different temperatures and pressures are tabulated in tables known every bit the steam tables. These are bachelor in hard copy or every bit software.
Case
Find the tables for super-heated steam at the back of your textbook.(Sonntag and Borgnakke 2012) (Note that water' refers to the chemical \(H_2O\) and is non an indication of the stage.
We talk of solid water, liquid water and water vapor when we refer to the solid, liquid or gas phases.)
Determine the specific book of steam at \(5000kPa\) and \(350^\circ C\). (\(0.05194 m^3/kg\)).
Now use the Platonic Gas Law to decide the specific volume (\(0.0575 m^three/kg\)). You can see in that location is a significant difference between the ii values.
Case
Steam at \(5000kPa\) has a specific volume of \(0.054 m^3/kg\). Find the temperature.
Solution
You volition note that in the table for super-heated h2o at \(5000kPa\), \(0.054 1000^3/kg\) lies between the specific volumes at \(350^\circ C\) and \(400^\circ C\). You need to interpolate to find the required temperature. (\(367.5^\circ C\))
Liquids and solids
The specific volume of compressed liquid water as function of temperature and force per unit area can be plant in the steam tables. Run across Borgnakke Table B.i.4 (Sonntag and Borgnakke 2012). Note that an increase in pressure has nigh no effect on the specific volume of liquid h2o. For a ten fold increment in pressure level (from \(500kPa\) to \(5000kPa\)) for water at \(20^\circ C\) the specific volume changes from \(0.001002 m^3/kg\) to \(0.001000 m^iii/kg\). Therefore, liquids (and solids) are normally considered to be in-compressible. From the table information technology is as well clear that the specific volume of water does increment somewhat with an increase in temperature. Information technology is therefore common practice to take the specific volume of compressed liquid water at \(T\) and \(P\), to be equal to the specific volume of saturated liquid water at temperature \(T\), even though the pressure level of saturated liquid water will be different to \(P\).
The volume of saturated solid h2o (ice) as role of temperature can likewise be constitute in Borgnakke Table B.1.5 (Sonntag and Borgnakke 2012). Water ice can also be assumed to exist in-compressible. For other substances, detailed tables are usually not available. Even so, the density of several liquids and solids at room temperature can be constitute in textbooks Table A.3 A.iv (Sonntag and Borgnakke 2012).
Example
Detect the specific volume of water at \(120^\circ C\) and \(5000kPa\) using the saturated water tables.
Solution
Using the temperature and force per unit area of the water to find the position of the water on a pressure level-temperature diagram (Effigy 2.2), it is articulate that the h2o is a compressed liquid. The specific volume of saturated liquid water at \(120^\circ C\) is \(0.001060m^3/kg\). Assuming liquid water to exist in-compressible, the specific book at \(5000kPa\) is therefore too taken as \(0.001060m^3/kg\) even though the saturation pressure is merely \(270.1kPa\).
It is left to the reader to compare this value to the value at \(5000kPa\) and \(120^\circ C\) from the Compressed liquid Tabular array B.1.4 (Sonntag and Borgnakke 2012).
Two-phase systems
Nosotros will first consider a system consisting of liquid water and water vapor.
Phase alter
If nosotros oestrus up liquid water enough it will get-go to eddy - it will undergo a phase change. Information technology is instructive to written report some of the events that occur equally a pure substance undergoes a phase change. Consider h2o at \(101.325kPa\) in a piston-cylinder assembly. The water is at 20\(^\circ\)C, a temperature lower than the boiling betoken and therefore information technology is a single-stage system. Information technology has two degrees of freedom. The temperature and the force per unit area can be varied independently without the h2o changing its stage. The h2o is heated while the force per unit area remains abiding at 101.325\(kPa\). The volume increases slightly as the h2o is heated and the temperature rises. (Assume the combined effect of the cylinder and the ambient pressure level is 101.325\(kPa\) and the piston is frictionless and can therefore move to suit whatsoever increase in volume.)
At the boiling point (\(100 ^\circ C\)), vapor volition outset to form. At the humid signal, when the first molecule of liquid water is about to exist transformed into a vapor, the quality (run across Paragraph 1.iii.2) is withal equal to aught and the liquid is chosen a saturated liquid. Equally more estrus is added more than vapor forms. All the heat that is added to the organisation is used to modify the liquid into vapor and the temperature remains abiding. Information technology is no longer possible to vary temperature and pressure independently without the system irresolute phase. If we increase the pressure on the system (by for instance putting additional weights on the piston) the vapor will condense, release estrus, and a single-phase organisation will outcome once again. If we resume heating at this college pressure level, the temperature volition rise to a college value (as previously) earlier vapor will starting time to form again. All the liquid will eventually vaporize. When the last liquid molecule vaporizes, the phase is called a saturated vapor. If the saturated vapor is heated, its temperature will rise and super-heated vapor will grade. The abiding pressure heating of liquid water at various pressures is shown as dashed lines in Figure ii.iii beneath.
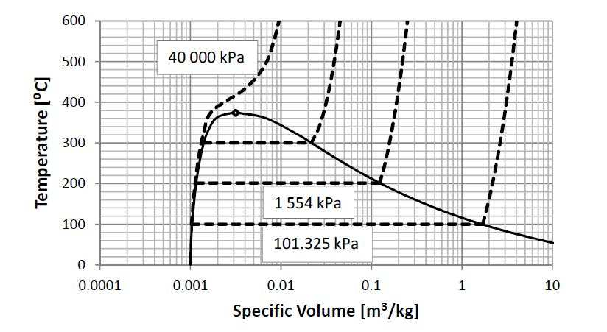
Figure 2.3: Constant pressure level heating of h2o.
If the pressure is loftier plenty, no stage separation will take identify. The liquid will change from a liquid-like phase to a gas-similar phase without two phases forming. Y'all can run into this happening in Effigy two.iii at \(40000kPa\). The minimum pressure where no phase separation takes place, is called the critical pressure. The temperature at the critical force per unit area is called the critical temperature. The critical pressure of water is \(22.09MPa\) and the disquisitional temperature \(374.14^\circ C\). Every bit long as 2 phases are present, the system is at the saturated land. The liquid is chosen saturated liquid and the gas, saturated vapor. The temperature is the saturation temperature and the force per unit area, the saturation force per unit area or vapor force per unit area. This condition is often too chosen an vapor-liquid equilibrium mixture.
On a \(P-v\) diagram Figure 2.5 the constant pressure heating of water volition be a horizontal line. The constant pressure heating of water can also be shown as a horizontal line on a T-P stage diagram (Figure two.2) The liquid-gas phase boundary in Figure 2.2 ends in the critical betoken.
It is clear from Figure 2.2 that the equilibrium force per unit area is a unique office of temperature10 and that, for a two-phase mixture, temperature and force per unit area are no longer independent. Once the force per unit area (or temperature) is specified, the temperature (or pressure) and the specific volumes of the saturated vapor and the saturated liquid are stock-still. This seems to imply that vapor/liquid two-phase organization only has ane caste of freedom considering all the variables are fixed once one variable is fixed. This is true for the intensive variables: \(T_{sat}, P_{sat},\) \(v_{sat,vapor},\) \(v_{sat,liquid}\).
Case
Find the saturation force per unit area, specific volume of saturated water vapor and specific volume of saturated liquid water at \(100^\circ C\). The saturation force per unit area as part of temperature can be constitute in Table B.1.1 of Cangel (Cangel and Boles 2002) (\(101.325kPa; ane.6729 m^3/kg; 0.001044 m^3/kg\))
In general we need to know the relative amount of liquid and vapor. We therefore need another variable - bringing to two the number of variables necessary to fully quantify the system. The second variable tin be specific book of the mixture or a variable that we will call quality.
Quality
For a saturated liquid-vapor mixture, the quality \((x)\) is the ratio of the mass of vapor to the full mass of the two-stage mixture:11
\[x=\frac{m_{vapor}}{m_{liquid}+m_{vapor}}\]
The value of the quality varies from cipher to unity. For a saturated liquid, \(ten=0\), and for a saturated vapor, \(10=1\). Quality is but divers for the saturated condition.12 Using the saturation tables and the definition of quality, the specific volume of a two-phase liquid-vapor mixture can be adamant:
\[\begin{equation} five=(one-10)v_f +10 v_g \tag{2.one} \terminate{equation}\]
Example
Decide the pressure and specific book of water at 100\(^{\circ}\)C with a quality of \(0.7\).
Solution
Because the quality has a value between zero and one, we know it is a two-phase mixture and the pressure will be the saturated pressure at 100\(^{\circ}C\), \(101.3kPa\). The specific book of the two phase mixture is calculated using Equation i.1 and the volumes of saturated liquid and saturated vapor at 100\(^\circ C\). ( \(1.171343 m^iii/kg\))
It is also possible to get liquid/solid equilibrium and vapor/solid equilibrium – as shown in Effigy 2.ii. Information technology is also possible to get equilibrium betwixt 3 phases - vapor, liquid and gas. It is the triple betoken and according to the Gibbs phase dominion, a pure substance has simply one such triple bespeak: at the intersection of the iii stage boundary lines – every bit tin be seen in Figure two.2.
If the pressure, temperature and specific book characteristics of water are plotted on three perpendicular axes, i each for temperature, pressure and specific volume, a iii dimensional shape results as shown in Effigy 2.four beneath.13
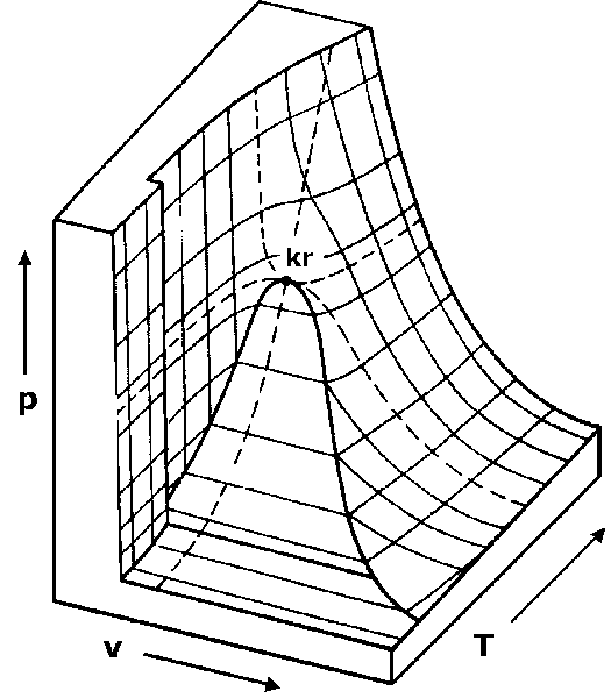
Figure ii.four: PVT diagram for water.
Determining the stage of h2o
It is necessary to provide numerical values for two of a possible four variables in social club to set up the country of a substance. The four variables are: Pressure, Temperature, Specific volume and quality. In order to determine the values of the unknown variables, first we get-go need to decide the phase (solid, liquid or gas) of the substance. In one case we know the phase, nosotros know which table (compressed liquid, saturated liquid, super-heated vapor) to use. Let us expect at mutual combinations of variables used to fix the state and how to make up one's mind the phase.
Temperature and pressure
The numerical values for temperature and pressure are supplied/specified. The stage is determined by comparing the specified temperature to the saturation temperature at the specified pressure level and/or comparing the specified force per unit area to the saturation pressure at the specified temperature. In effect this means plotting the country on a Pressure–Temperature Phase diagram. Just 3 phases are possible when the pressure and temperature are specified: solid, liquid and gas. As mentioned earlier, the lines separating the phases equally in Figure 2.2 has zero thickness and the land will either be a solid OR a liquid OR a vapor.
The slope of the solid/liquid equilibrium line for water on a pressure-temperature graph has a very large negative gradient. This means liquid water under high force per unit area volition freeze at a slightly lower temperature than water under a lower pressure level. (Most other substances contracts upon freezing and the slope of the solid/liquid boundary is positive.)14 Due to the negative gradient of the solid/liquid phase boundary, the temperature of the triple point of water is \(0.01^\circ C\) while the melting indicate of water ice at \(100kPa\), is \(0^\circ C\). In this notes information technology is causeless that the phase purlieus between ice and liquid water is vertical and that ice melts at \(0^\circ C\) at any pressure.15
Consider water at \(100kPa\) and \(l^\circ C\) – the \(\Box\) in Effigy 2.two. The specified temperature is lower than \(99.62^\circ C\), the saturation temperature at \(100kPa\) 16 and the specified pressure higher than \(12.34kPa\), the saturation pressure level at the specified temperature. The phase is therefore a compressed (or sub-cooled) liquid as is besides axiomatic from its position on the phase diagram. The quality is undefined and if we presume an in-compressible liquid, the volume of the substance is the same as that of the saturated liquid at \(fifty^\circ C\), \(0.001030\frac{grand^3}{kg}\), which can exist read from the tables for saturated water (Tabular array B.1.2).(Sonntag and Borgnakke 2012)
Consider h2o at \(100kPa\) and \(150^\circ C\) – the \(\circ\) in Figure 2.2. Its pressure is lower than \(475.9kPa\), the saturation force per unit area at the specified temperature and its temperature is higher than \(99.62^\circ C\), the saturation temperature at the specified pressure. This means it is an super-heater vapor (often also called a gas), which is too axiomatic from its position on the phase diagram. Again the quality is undefined and the specific volume tin can be read from the super-heated water vapor tables, \(1.93636\frac{m^3}{kg}\)
Pressure or temperature and specific book
The heating of compressed liquid water at a constant pressure level (lower than the critical force per unit area) will first effect in a saturated liquid, and then in a two-phase mixture, and then in a saturated vapor and and so in a super-heated vapor. The P-\(5\) stage diagram of h2o is shown in Figure 2.5 beneath. The solid water phase (ice) has been omitted from this phase diagram. Because liquid water expands upon freezing (as tin exist seen in Figure ii.4), the P-5 phase diagram showing the solid phase, would have been unnecessarily complicated.17
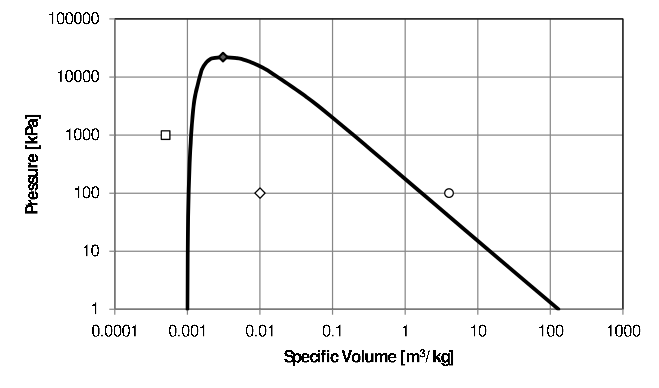
Figure 2.v: Pressure level-Specific Volume phase diagram for h2o.
Consider water at \(5000kPa\) and \(0.001000\frac{m^3}{kg}\) – the \(\Box\) in Effigy 2.5. It is a compressed liquid because its specific book is smaller than the specific book of the saturated liquid at the same pressure.xviii For a compressed liquid, quality is undefined. As the specific volume of a compressed liquid does non modify much with changes in temperature at lower values of temperature – equally can exist seen in Effigy 2.3, it may exist difficult to obtain an accurate value for temperature from specified values of pressure and specific volume.
Water at \(100kPa\) and \(0.01\frac{m^iii}{kg}\) (the \(\diamondsuit\) in Effigy ii.five) is a ii-phase mixture as its specific book lies between that of the saturated liquid and saturated vapor at \(100kPa\). Its quality can exist calculated from Equation (two.ane) using the specific volume of the saturated liquid (\(0.001043\frac{yard^3}{kg}\)), and the specific volume of the saturated vapor at \(100kPa\) (\(1.694\frac{m^3}{kg}\)) to obtain a value of \(x=0.005291\). The temperature is the saturation temperature at \(100kPa\), \(99.62^\circ C\).
Water at \(100kPa\) and \(four.02781\frac{m^iii}{kg}\) (the \(\circ\) in Figure 2.5) is a super-heated vapor as its specific volume is larger than that of a saturated vapor at the specified pressure level. Its temperature can be adamant from the super-heated h2o tables. In this case the temperature can be read directly from the tables (\(600^\circ C\)), merely in general, interpolation will be necessary. Quality is undefined for a super-heated vapor.
When the temperature and specific book are specified, the stage must start exist adamant by comparing the value of specified volume to the specific volume of the saturated liquid and and the specific book of the saturated vapor at the specified temperature - in upshot by plotting the country on a \(T-v\) diagram (Figure 2.5).
Temperature or pressure and quality
The quality of a saturated liquid is \(0\) and for a saturated vapor, \(1\). As quality is undefined for a sub-cooled liquid and super-heated vapor, if the quality is specified, it means it is a two-phase mixture and the temperature (or pressure) for the specified pressure (or temperature) can be read from the tables for saturated water and the specific volume determined from Equation (2.1). An instance is done in Paragraph 2.3.2
Unit conversion
It has been stated previously that a pressure of one atmosphere is the same as \(101.325kPa\). Let us assume we know the pressure is \(100 atm\) and now need to know what the pressure is in \(kPa\). Because \(1atm=101.325kPa\), we know \(\frac{101.325kPa}{1atm}=1\). Now:
\[100atm = 100 atm \times \frac{101.325 kPa}{1 atm}= 10100 kPa\]
Note that the answer tin can only contain three significant digits. Sometimes psi (pound-force per square inch) is used as a pressure unit. Let usa calculate the value (in kPa) for a pressure level of 14.50psi. A pound-force is the weight of a mass of i pound in the gravitational field of the earth.
\[14.50psi=\frac{xiv.50lb_f}{i(inch)^two} \times \frac{four.448N}{1 lb_f} \times \frac{i( inch)^2}{(0.02540m)^2}=99.970kPa\]
Annotation that as simply four meaning digits is used the calculation, the answer can as well not be more that iv significant digits.
Y'all can ask Google: 'Convert psi to kPa' and become the conversion gene straight.
Source: https://www.bookdown.org/asvn90/Understanding-Thermodynamics/properties-of-pure-substances.html
0 Response to "what property of a substance corresponds to the average potential energy of its particles"
Post a Comment